IEEE 754 - стандарт двоичной арифметики с плавающей точкой
Автор: Яшкардин Владимир Леонидович
Сайт: www.softelectro.ru
Данный стандарт разработан ассоциацией IEEE (Institute of Electrical and
Electronics Engineers) и используется для представления действительных чисел
(чисел с плавающей точкой) в двоичном коде. Наиболее используемый стандарт для
вычислений с плавающей точкой, используется многими микропроцессорами и
логическими устройствами, а также программными средствами.
Полное название стандарта в ассоциации IEEE:
- IEEE Standard for Binary Floating-Point Arithmetic (ANSI/IEEE
Std 754-1985)
- IEEE стандарт для двоичной арифметики с плавающей точкой
(ANSI/IEEE Std 754-1985)
Название стандарта в международной электротехнической комиссии IEC:
- IEC 60559:1989, Binary floating-point arithmetic for
microprocessor systems
- IEC 60559:1989 двоичная арифметика с плавающей точкой для
микропроцессорных систем
- (IEC 559:1989 - старое обозначение стандарта)
В августе 2008 года ассоциация IEEE выпустила стандарт IEEE 754-2008, который
включил в себя стандарт IEEE 754-1985.
В настоящее время ассоциация IEEE
представляет собой коммерческое предприятие, а не общественную ассоциацию
инженеров от электроники. IEEE продает информацию по своим документам. Заплатив
77$(цены на март 2009 г.) вы получите документ описывающий стандарт ANSI/IEEE
Std 754-1985 в .pdf формате. Описание которое вы получите от IEEE скорее всего
только запутает вас, так как широкое использование получила только часть
стандарта, остальная часть стандарта малоприменима в технике и программировании
и усложняет целостное логическое описание стандарта. Я бесплатно, но доступно
опишу Вам применяемую часть стандарта IEEE754. Но если Вы считаете, что
бесплатная информация бесполезна, то можете перечислить любую сумму на
электронный кошелёк ресурса www.softelectro.ru. Эти пожертвования пойдут на
развитие этого некоммерческого ресурса (в частности на описание других
стандартов:-)
Описание стандарта.
Стандарт IEEE 754-1985 определят:
- как представлять нормализованные положительные и отрицательные числа с
плавающей точкой
- как представлять денормализованные положительные и отрицательные числа с
плавающей точкой
- как представлять нулевые числа
- как представлять специальную величину бесконечность (Infiniti)
- как представлять специальную величину "Не число" (NaN или NaNs)
- четыре режима округления
- пять исключений
IEEE 753-1985 определяет четыре формата представления чисел с
плавающей запятой:
- с одинарной точностью (single-precision) 32 бита
- с двойной точностью (double-precision) 64 бита
- с одинарной расширенной точностью (single-extended precision) >=43 бит
(редко используемый)
- с двойной расширенной точностью (double-extended precision) >= 79 бит
(обычно используют 80 бит)
Основное применение в технике и программирование получили форматы 32 и 64
бита. Например в основных логических языках VB и С используют типы данных single
и double. Далее я буду рассказывать в основном про формат single, так как double
является просто увеличенной копией single.
Основные понятия в представлении чисел с плавающей точкой.
Возьмем, к примеру, десятичное число 155.625
Представим это число в
нормализованном экспоненциальном виде : 1.55625*10^2 =1,55625e+2
Число
1,55625e+2 состоит из двух частей: мантиссы M=1.55625 и экспоненты e =+2
Если
мантисса находится в диапазоне 1<=M<2 то число считается
нормализованным.
Экспонента представлена основанием системы исчисления (в
данном случае 10) и порядком (в данном случае +2).
Порядок экспоненты может
иметь отрицательное значение, например число 0,0155625=1,55625e-2.
Преобразование десятичного числа в двоичное с плавающей точкой.
Наша задача сводится к представлению десятичного числа с плавающей точкой, в
двоичное число с плавающей точкой в экспоненциальном нормализованном виде:
155.625 = 1*2^7 +0*2^6+0*2^5+1*2^4+1*2^3+0*2^2+1* 2^1+1*
2^0+1*2^-1+0*2^-2+1*2^-3
155.625 =128 + 0 + 0 + 16 + 8 + 0 + 2 + 1 + 0.5 + 0
+ 0.125
155.625 = 10011011.101 - число в двоичной системе с плавающей
точкой
1.55625e+2=1.0011011101e+111- число в нормализованном экспоненциальном
виде
В результате мы получили в двоичном коде:
- M=1.0011011101 (мантисса)
- e= +111 (экспонента по основанию 2)
Преобразование двоичного числа с плавающей точкой в 32 битный формат
IEEE754
В принципе всё готово чтобы представить число в 32
битовом формате, но есть тонкости:
- Число может быть +/- . Поэтому отведем 1 бит для обозначения знака числа:
0-положительное, 1-отрицательное (этот бит будет самый старший в 32 битной
последовательности)
- Далее пойдут биты экспоненты, для этого выделим 1 байт (8 бит), но
экспонента тоже может быть +/- Для определения знака экспоненты, чтобы не
вводить ещё один бит знака, добавим смещение к экспоненте +127(0111 1111 - это
половина пространства отведенного под экспоненту). То есть, если наша
экспоната = +7 (+111 в двоичной), то смещенная экспонента = 7+127=134. А если
бы наша экспонента была -7 , то смещенная экспонета=127-7 =120. Смещенную
экспоненту мы и будем записывать в отведенные 8 бит. При этом, когда нам будет
нужно получить экспоненту, мы просто отнимем 127 от этого байта.
- Оставшиеся 23 бита мы отводим для мантиссы. Но, у нормализованной двоичной
мантиссы первый бит всегда равен 1, так как число лежит в диапазоне
1<=M<2. Нет смыла, записывать единицу в отведенные 23 бита, поэтому в
отведенные 23 бита мы запишем остаток от мантиссы.
В результате мы получим число 155.625 в 32- битном формате IEEE754:
| 1 бит
| 8 бит
| 23 бит
| 32 бит
|
| 0
| 1000 0110
| 001 1011 1010 0000 0000 0000
| = 43 1B A0 00 (hex)
|
| 0(dec)
| 134(dec)
| 1810432(dec)
|
|
| знак числа +
| смещенная экспонента
| остаток от мантиссы
| число 155.625 в формате IEEE754 |
Из этого 32 битного числа мы сможем восстановить десятичное число с плавающей
точкой, так как мы знаем все параметры представленного числа.
Приведу формулу для восстановления числа из стандарта IEEE754 для одинарной
точности (single):
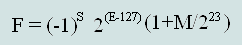
где:
- S- бит знака (31 бит)
- E- смещенная экспонента (23-30 биты)
- M - остаток от мантиссы (0-22 биты)
- F- десятичное число с плавающей точкой
Проверяем:
F =(-1)^0*2^(134-127)*(1+ 1810432/8388608)=
2^7*(1+0,2158203125)=128*1,2158203125=155.625
Вывод этой формулы приводить
не буду, всё видно и так. Поясню только (1+ M/2^23) - это мантисса, единица в
этой формуле- это та единица, которую мы выбросили из 23 бит, а остаток мантиссы
в десятичном виде находим отношением двух целых чисел - остатка мантиссы к
целому)
Формальное представление нормализованных чисел в формате IEEE 754.
Рис. 1 Представление формата числа в стандарте IEEE 754
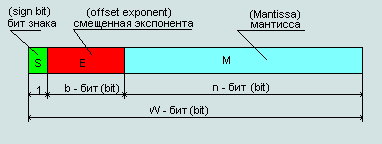
где:
- S - бит числа S=0 - положительное число; S=1 - отрицательное число
- E - смещенная экспонента; exp = E - 2^(b-1) + 1 , где
exp - экспонента
двоичного нормализованного числа с плавающей точкой
2^(b-1)-1 - смещение
экспоненты
- M - остаток мантиссы двоичного нормализованного числа с плавающей точкой
Формула вычисления десятичных чисел с плавающей точкой,из чисел
представленных в стандарте IEEE754:
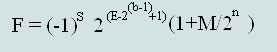 Формула №1
Формула №1
Рис.2 Формат числа одинарной точности (single-precision) 32 бита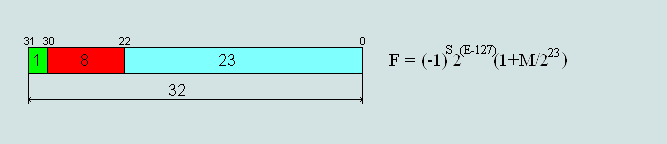
Рис.3 Формат числа двойной точности (double-precision) 64 бита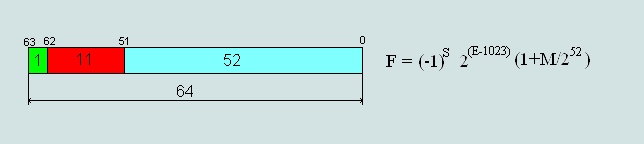
Исключения чисел формата IEEE754 из алгоритма вычисления по формуле №1.
Если применить формулу 1 для вычисления минимального и максимального числа
представленного в IEEE754, то получим следующие результаты:
- 00 00 00 00 hex= 5,87747175411144e-39
(минимальное положительное число)
- 80 00 00 00 hex=-5,87747175411144e-39
(минимальное отрицательное число)
- 7f ff ff ff hex= 6,80564693277058e+38
(максимальное положительное число)
- ff ff ff ff hex=-6,80564693277058e+38
(максимальное отрицательное число)
Отсюда видно, что невозможно представить число нуль в заданном формате.
Поэтому из стандарта сделаны исключения и формула №1 не применяется в
следующих случаях:
1. число IEEE754=00 00 00 00hex считается числом +0
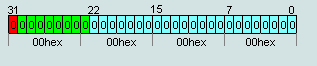 Рис.4
Рис.4
число IEEE754=80 00 00 00hex считается числом -0
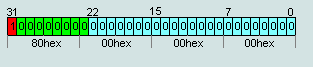 Рис.5
Рис.5
2. число IEEE754=7F 80 00 00hex считается числом +∞
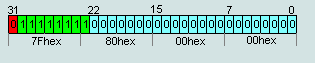 Рис.6
Рис.6
число IEEE754=FF 80 00 00hex считается числом -∞
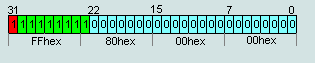 Рис.7
Рис.7
3. числа IEEE754=FF (1xxx)X XX XXhex не считается числами (NAN), кроме случая
п.2
числа IEEE754=7F (1xxx)X XX XXhex не считается числами
(NAN), кроме случая п.2
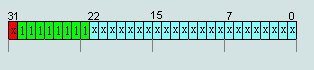 Рис.8
Рис.8
Число представленное в
битах с 0...22 могут быть любым числом кроме 0.
4. числа IEEE754=(x000) (0000) (0xxx)X XX XXhex считаются денормализованными
числами, за исключением чисел п.1 , то есть -0 и +0
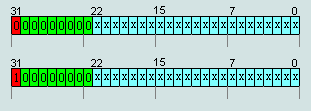 Рис.9
Рис.9
Формула расчета денормализованных чисел:
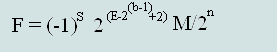 (Формула №2)
(Формула №2)
Пояснения к исключительным числам:
- С нулем понятно. Без него никак нельзя. Смущает только наличие двух нулей.
Думаю, это было сделано для симметричности.
- - ∞/ +∞ , тоже понятно. Числа, которые больше границ диапазона
представления чисел считаются бесконечными.
- Не числа NAN(No a Numbers). К ним относятся символы, или результаты
недопустимых операций.
- Денормализованные числа. Это числа, мантиссы которых лежат в диапазоне 0.1
<= M <1 Денормализованные числа находятся ближе к нулю, чем
нормализованные. Денормализованные числа как бы разбивают минимальный разряд
нормализованного числа на некоторое подмножество. Сделано так потому, что в
технической практике чаще встречаются величины близкие к нулю.
Границы диапазонов нормализованных и денормализованных чисел:
Рис. 10 Минимальное нормализованное число (абсолютное)
00 80 00 00 =
2^-126*(1+0/2^23)=2^-126 = 1,17549435e-38
80 80 00 00 =
-2^-126*(1+0/2^23)=2^-126=-1,17549435e-38
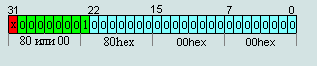 Рис.10
Рис.10
Рис. 11 Максимальное денормализованое число (абсолютное)
00 7F FF FF =
2^-126*(1-2^-23) = 1,17549421e-38
80 7F FF FF = -2^-126*(1-2^-23)
=-1,17549421e-38
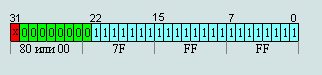 Рис.11
Рис.11
Из рис. 10 и 11
видно что минимальное нормализированное число граничит с максимальным
денормализированным.
Рис. 12 Минимальное денормализованное число (абсолютное)
00 00 00 01 =
2^-126* 2^-23= 2^-149 = 1,40129846e-45
80 00 00 01 = -2^-126* 2^-23= 2^-149 =
- 1,40129846e-45
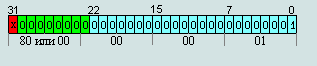 Рис.12
Рис.12
Это число граничит с
нулем.
Рис.13 Максимальное нормализированное число (абсолютное)
7F 7F FF FF =
2^127*(2-2^-23) = 3,40282347e+38
FF 7F FF FF = -2^127*(2-2^-23)= -
3,40282347e+38
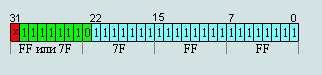 Рис.13
Рис.13
Это число граничит с
бесконечностью.
Представим полный диапазон чисел представленных в формате 32 бит по
стандарту IEEE754:
Рис.14 Диапазон чисел формата 32 бита представленных по стандарту IEEE
754
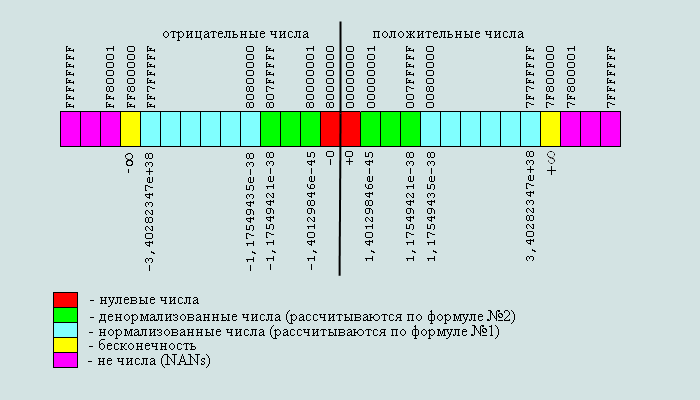
Таблица 1. Сведенья о формате 32/64 бит в стандарте ANSI/IEEE Std
754-1985
| наименование формата
| single
| double
|
| длина числа, бит
| 32
| 64
|
| смещенная экспонента (E), бит
| 8
| 11
|
| остаток от мантиссы (M), бит
| 23
| 52
|
| смещение
| 127
| 1023
|
| формула расчета денормализованых чисел
| F =(-1)^S*2^(E -126)* M/2^23
| F =(-1)^S*2^(E -1022)*M/2^52
|
| формула расчета нормализованных чисел
| F =(-1)^S*2^(E-127)*(1+ M/2^23)
| F =(-1)^S*2^(E-1023)*(1+M/2^52)
|
| минимальное число
| ±2^-149=±1,40129846e-45
| ±2^-1074= ± 4,94065646e-324
|
| максимальное число
| ±2^127*(2-2^-23) = ± 3,40282347e+38
| ±2^1023*(2-2^-52) = ± 1,79769313e+308 |
Заключение.
Стандарт IEEE 754 широко применяется в технике и программировании. При этом
хочется отметить, что в нем заложены существенные недостатки. Создается
впечатление, что в разработке стандарта не принимали участие профессиональные
математики. Директор института математики и ее применений в Миннеаполисе, США
Дуглас Н.Арнольд утверждает, что целый ряд крупнейших аварий с человеческими
жертвами и миллиардными убытками всецело обязан нынешней технологии компьютерных
вычислений и представлений данных по стандарту IEEE 754.
Вы можете прочитать об этом в статье IEEE754-тика угрожает человечеству
Как программист скажу, никогда не применяйте одинарную точность (single) в
программах, если полностью не представляете и не контролируете всю процедуру
расчета, так как результат компьютерного расчета может быть не предсказуем. На
одной из крупных научных конференций ректор Технического университета Вены проф.
П. Скалички заявил, что "с тех пор, как подробнее узнал о принятых способах
выполнения машинных вычислений, очень опасается ходить по мостам и оказываться
внутри других сложных инженерных сооружений".
Формат чисел IEEE754 неплохо работает в технике, когда нужно представить и
передать число, но требует абсолютного контроля в операциях деления и
умножения.
Вот пример, который вы можете испытать:
Программный код в VB который делит
два одинаковых числа 0,3 : 0,3 = 1 (это должно получится)
Private Sub Command1_Click()
Dim a, c As Single
a = 0.3
c = 0.3
Text1.Text = c /
a
Text2.Text = a / c
End Sub
Рис.15 Вот результат вычислений этой программы:
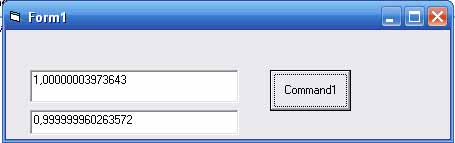
a=0.3 c=0.3 c : a = 1.00000003973643
a=0.3 c=0.3 a : c =
0.999999960263572
Здесь вы видите не только не точный результат, но и
зависимость результата от расположения переменных. Это только одна операция,
представьте, что операций тысячи. Результат таких вычислений будет не
предсказуем.
Вот ещё пример: Text1.Text = (c / a - 1) * 10000000000
Если посчитать на
бумажке ответ будет = 0, а если на компьютере = 397,364299242753
Как Вы
считаете- есть ли разница между 0 и 397 (допустим в ядерных бомбах!)
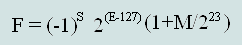

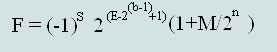 Формула №1
Формула №1

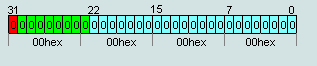 Рис.4
Рис.4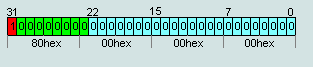 Рис.5
Рис.5 Рис.6
Рис.6 Рис.7
Рис.7 Рис.8
Рис.8 Рис.9
Рис.9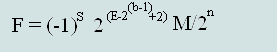 (Формула №2)
(Формула №2)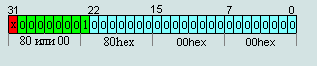 Рис.10
Рис.10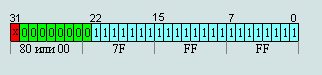 Рис.11
Рис.11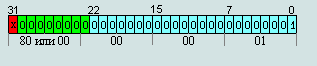 Рис.12
Рис.12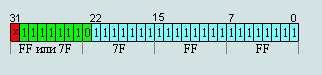 Рис.13
Рис.13
